Sekumpulan data kuantitatif yang tidak dikelompokkan dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukan simpangan rata-rata (SR) dengan menggunakan rumus :
dan juga rumus
Contoh Soal 1 :
Hitung simpangan rata-rata dari data kuantitatif berikut :
12, 3, 11, 3, 4, 7, 5, 11
Pembahasan :
Jadi, simpangan rata-ratanya adalah 3,25.
Contoh Soal 2 :
Hitunglah simpangan rata-rata nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka seperti Tabel 1.
Tabel 1. Nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka
Interval Kelas
|
Frekuensi
|
40 – 44
|
3
|
45 – 49
|
4
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
2
|
90 – 94
|
2
|
Penyelesaian :
Kelas
Interval
|
Nilai Tengah (xi)
|
fi
| ||
40 – 44
|
42
|
3
|
23,7
|
71,1
|
45 – 49
|
47
|
4
|
18,7
|
74,8
|
50 – 54
|
52
|
6
|
13,7
|
82,2
|
55 – 59
|
57
|
8
|
8,7
|
69,6
|
60 – 64
|
62
|
10
|
3,7
|
37
|
65 – 69
|
67
|
11
|
1,3
|
14,3
|
70 – 74
|
72
|
15
|
6,3
|
94,5
|
75 – 79
|
77
|
6
|
11,3
|
67,8
|
80 – 84
|
82
|
4
|
16,3
|
65,2
|
85 – 89
|
87
|
2
|
21,3
|
42,6
|
90 – 94
|
92
|
2
|
26,3
|
52,6
|
Σfi = 71
|
Jadi, simpangan rata-rata (SR) = 671,7 / 71 = 9,46.
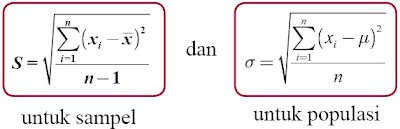
Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn. Dari data tersebut, dapat diperoleh nilai simpangan baku (S) yang ditentukan oleh rumus berikut.
Contoh Soal 3 :
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Kunci Jawaban :
Jadi, simpangan bakunya adalah 5,83.
Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh x1, x2, …, xn dan masing-masing data mempunyai frekuensi f1, f2, …, fn. Simpangan baku (S) dari data tersebut diperoleh dengan menggunakan rumus :
Contoh Soal 4 :
Hitunglah simpangan baku dari nilai ulangan Fisika dari 71 siswa kelas XI SMA Merdeka sesuai Tabel 1.
Jawaban :
Dari hasil perhitungan sebelumnya diperoleh µ = 65,7.
xi
|
fi
|
xi - µ
|
(xi - µ)2
|
Σfi (xi - µ)2
|
42
|
3
|
–23,7
|
561,69
|
1.685,07
|
47
|
4
|
–18,7
|
349,69
|
1.398,76
|
52
|
6
|
–13,7
|
187,69
|
1.126,14
|
57
|
8
|
– 8,7
|
75,69
|
605,52
|
62
|
10
|
–3,7
|
13,69
|
136,9
|
67
|
11
|
1,3
|
1,69
|
18,59
|
72
|
15
|
6,3
|
39,69
|
595,35
|
77
|
6
|
11,3
|
127,69
|
766,14
|
82
|
4
|
16,3
|
265,69
|
1.062,76
|
87
|
2
|
21,3
|
453,69
|
907,38
|
92
|
2
|
26,3
|
691,69
|
1.383,38
|
Σfi = 60
|
Σfi (xi - µ)2 = 9.685,99
|
Jadi, simpangan bakunya σ :
c. Variansi (Ragam)
Untuk data yang tidak dikelompokkan ataupun data yang dikelompokkan, diperoleh nilai variansi (v) dengan
menggunakan rumus:
Contoh Soal 5 :
Hitunglah variansi dari data Contoh 3.
Pembahasan :
Dari hasil perhitungan Contoh 3. diperoleh S = 5,83 maka :
v = S2 = (5,83)2 = 33,99.
Sumber : http://perpustakaancyber.blogspot.com/2013/04/rumus-simpangan-baku-simpangan-rata-rata-ragam-variansi-koefien-keragaman-contoh-soal-jawaban-statistik-matematika.html#ixzz2iBBTeCE9




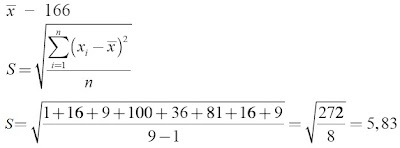


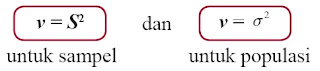
thanks yaa,
BalasHapussangat membantu sekali penjelasannya mudah dimengerti dan rinci...
Kalau boleh nyaran sih, fokusnya juga kepada simpangan Baku, bingung nih... Bagaimana pembahasan terlalu singkat.
BalasHapusSemoga kedepannya bisa lebih bertahap, Terima Kasih.
terima kasih
BalasHapussalam kenal
BalasHapusBisa kah di jelaskan cara mencari rata-rata dari 70 dengan simpangan 7
BalasHapusterimakasih
BalasHapusTerima Kasih Gan, simple, jelas, dan sangat sangat bermanfaat untuk saya.....
BalasHapusthank yah buat rumus-rumusnya
BalasHapussukses yah buat blog nyah
gak ngerti tid
BalasHapusTerimakasih atas pencerahannya gan :D
BalasHapusAgak bingung :/ tapi trima kasih :)
BalasHapusSerius gan zonk kali gdk yg d mengerti, terlalu simpel
BalasHapusMakasih banget :))
BalasHapusterimah kasih, sdah sangat membantu
BalasHapusthanks ya.. membantu banget
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusThanks sudah membantu,akan tetapi masih ada kekurangan di contoh soal 3 simpangan baku. Tertulis 9 sempel, tetapi saat dimasukkan hanya ada 8 sempel. Itu aja, thanks
BalasHapusmembantu banget gan
BalasHapusmakasih ya sangat membantu
BalasHapusthanks ya membantu banget
BalasHapusmaaf mau tanya, untuk contoh no 3,angka 1,16,9 ,100,36,81,16,9 itu dari mana ya?
BalasHapusItu didapat dari pengurangan | X - (rata-rata) |
HapusEx : | 165 - 166 |^2 + | 170-166 |^2 + | 166 - 169 |^2 dst
Hasilnya :
= 1^2 + 4^2 + 3^2 dst
= 1 + 16 + 9 dst
Kenapa hasilnya bukan min - ?
Karna tanda ini | | berarti bilangan mutlak (Tanpa tanda min / plus)
Thanks,sangat membantu
BalasHapussalah di perhitungan simpang bakunya, masa 272
BalasHapustrims...
BalasHapussebagai masukan saja biar lbh jelas ...apakah....contoh X-X(bar) = 165-166 = -1, dan 42-65.7 = -23,7...apakah seperti itu...supaya tanda min dn plusnya diperhatikan karena mempengaruhi hasil.trima kasih
BalasHapusTidak . Karna itu memakai kurung | | yang berarti nilai mutlak (nilai yang tidak memakai plus/minus)
Hapussaya lihat contoh soal disimpangan rata-rata (Sr) dilihat dari rumusnya ..trima kasih
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusAgak bingung, tapi terimakasihh.
BalasHapusKalau boleh tanya di rumus variansi kan tertulis untuk sampel dan populasi, nah maksud sampel dan populasi itu yg bagaimana ya mbak?
What are the best casino games?
BalasHapusBest 라이브 바카라 Casino Games Online · 888casino · 실시간 배팅 사이트 Royal 해외 라이브 스코어 Panda · Rainbow Riches · Jackpot 6000 · Play'n GO · PlayOJO · Mr Green netteller · Play'n 안전 바카라 사이트 Go · PlayUp